Genel algoritma kavramının kesin bir şekilde belirlenmesi ve ortak tanımının yapılması Turing makinası kavramının ortaya çıkmasıyla mümkün olmuştur. Turing makinası kavramı, 1937 yılında İngiliz matematikçisi, şifre uzmanı ve bilgisayar bilimcisi Alan Mathison Turing (1912-1954) tarafından bulunmuştur. Alan Turing, Hilbert problemine çözüm getirebilmek amacıyla Turing makinasını ortaya koymuştur. Turing, insan beynini bir ‘makine’ gibi görüp, ‘makina’ kavramını tanımlamak amacıyla, işlevlerini temel öğelerine ayırmıştır. Böylece bir matematik problemi ile uğraşan matematikçinin eylemlerini, ‘mekanik yöntemler’ olarak belirlemiştir.
Bir Turing makinası kuramsal bir makinadır. Bir fiziksel nesne değil, bir ‘soyut matematik’ ürünüdür. Öklid Algoritması’ nda sayılar ne kadar büyük olursa olsun algoritma yine sonlu komutlar dizisinden oluşur. Sayıların büyük olması yöntemin daha uzun bir zamanda cevap vermesini sağlayabilir. Ayrıca işlemlerin yapılabilmesi için daha fazla ‘müsvedde kağıdı’ gerekebilir.
Turing makinası işlemler için sınırsız dışsal veri biriktirme (müsvedde kağıdı) alanından yararlanabilir ve ‘sınırsız çıktı üretebilir. Dışsal veri biriktirme alanına işlemlerin sonuçları kaydedilir. Turing makinası birbirinden farklı ve sonlu durumlar dizisine sahiptir. Bunlara makinanın içsel durumları denir. Makinanın davranışı bu içsel durumlar ve girdi tarafından kontrol edilir.
Girdi, çıktı ve hesaplama işlemi daima sonlu olmalıdır. Turing makinasının dışsal veri bellek alanını sonsuz bir bant şeklinde düşünebiliriz. Bandın üzerindeki işaretleri makinabelirleyebilir, değiştirebilir, silebilir. İşlemlerin bir çoğunda sonuçlar, yeni veriler gibi kullanılabildiğinden banın girdi ya da müsvedde kağıdı gibi görev yapması sağlanır. Bant sonsuz uzun olsa da üzerindeki işaretlerin sayısı sonsuz olamaz. Bant ileri geri harekat edebilir ve belirli bir noktadan sonra bant tümüyle boş olmalıdır.
Alan Turing, makinasının okuma işlemini bandın ileri-geri (yani sağa-sola) hareketi sayesinde olması gerektiğini düşünmüştür. Makinanın bant üzerinde ‘bir’ kare okuyup sonra sağa ya da sola kaydığını düşünebiliriz.
![]()
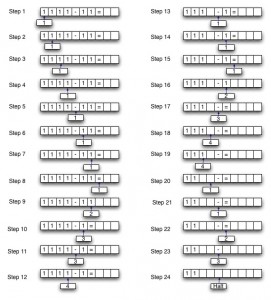
N kare okuyan ve M kare kayan Turing makinalerı da bir defada bir kare okuyan ve kayan makinalar cinsinden kolayca modellenebilir. İçsel durumlarını 0, 1, 2, 3, … ile gösterirsek bir Turing makinasının çalışma sistemine aşağıdaki gibi bir örnek verebiliriz. Okun sol tarafındaki ‘büyük’ rakam bandın üzerindeki işaretler ve okuma işleminin gerçekleştiğini belirtir.
Makina bu rakamın yerine sağ taraftaki ‘büyük’ rakamı koyar. R, bandın sağa doğru bir adım, L andın sola doğru bir adım hareket ettiğini gösterir. Stop ise işlemin tamamlandığı anlamına gelir.
01–> 13 1 L komutunu ele alalım. Makina, 0 durumunda ve banttan 1 okur ve 13 numaralı içsel duruma geçerek 1′ i 1 olarak bant üzerinde bırakır. Ve bant bir kare sola kayar.
2591—> oOR STOP 259 numaralı içsel durumda 1 okur. O numaralı içsel duruma geçip 1′ i silerek bant üzerine 0′ ı bırakır ve sağa doğru bir kare kayarak işlem tamamlanır.
İçsel durumlar ikilik sistem kullanılarak da ifade edilebilir. Bu durumda Turing makinalarıne örnek çalışma sistemi aşağıdaki gibi olur.
Basit Giriş:
1
4
0 1 0 1 1 0 9 -1 1
9 -1 2 9 -1 3 9 -1 -2
9 -1 -1 9 -1 -2 9 -1 -2
9 -1 -2 9 -1 -2 9 -1 -2
010100
Uygun Çıkış:
Kabul: 0101999
Turing makinasının bir seferde bir kare okuması ve tek boyutlu bandın bir kare hareket etmesi durumu akla değişik alternatiflerin gelmesini sağlayabilir. Daha farklı alternatifler veya sistemler kullanılabilir. Örneğin birbirleriyle bağlantılı ve aynı anda çalışan çok sayıda bant (belki 10 belki 1000 bant) düşünülebilir. İki bant sayesinde, iki boyutlu bir düzlemdeki iki koordinat elde edilebilir. Böylece iki bandın kullanımı ile iki boyutlu düzlemin kullanımı özdeştir. Yine de bütün bunlar, algoritmalar ile yapılan işlemleri değiştirmez.
Makina, ihtiyaç olan boş alanı bant üzerinde bulduğu sürece, tek bant yeterlidir. Bu tarz bir kodlama elverişsiz görünse de ilke olarak sonucu sınırlamaz. Birbiriyle iletişimli iki makina aslında bir makina demektir. Ve iletişimli olmayan iki ayrı makinadan daha fazlasını gerçekleştiremez. Böylece birden fazla Turing makinasının paralel çalıştırılması bazı durumlarda çalışma hızını olumlu etkilese de ilke olarak yine bir şey kazandırmaz.
Evrensel Turing Makinası
Alan Turing’ in herhangi bir Turing makinasının (T) hesaplayabildiği her şeyi işleyen bir evrensel Turing makinasının (U) yapılabileceğini kanıtlaması yaptığı büyük katkılardan biridir.
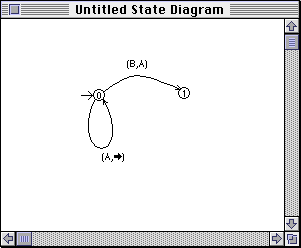
T Turing makinasının komut dizisi ikilik sistemde bant üzerine kodlanmıştır. Bu bant evrensel Turing makinasının girdilerinin ilk kısmını oluşturur. Yani T’ yi taklit etmesi için bandın başlangıç kısmı, bütün verileri U’ ya verir. Bir f(x) fonksiyonu işleyen her T Turing makinası için bir dT işaretler dizisi vardır.
Bant üzerine bir şeyin kaydedilip kaydedilmediğini gösterir. X girdisi dT işaretler dizisinin izlediği bir banda kaydedilmiş ise ve U, bir q durumunda ise dT’ nin en solundaki işareti etkiler ve bant f(x) değerini verir.
![]()
Turing makinası ne kadar karmaşık olursa olsun Evrensel Turing makinası bu durumu hesaplayabilir. T, U makinesinden daha çok durum içerse de, ya da T’ nin daha geniş bir işaretler dizisi olsa da sonuç değişmez. Bu işlem için U’ nun T makinasını U’ ya tanıtan dT işaretler dizisini içermesi yeterlidir. Evrensel Turing makinası evrensel bir taklitçidir. Bir Turing makinasının işlediği her şeyi hesaplayabilir. Evrensel Turing makinesi “hesaplanması bilinen” her şeyi hesaplayabilen bir makinedir. Evrensel T makinesi hesaplanabilen kavramları tanımlamaya yarar. Bir Turing makinası tarafından üretilebilen sayılara ‘hesaplanabilir’ sayılar denilirken, bir Turing makinası tarafında üretilemeyen sayılara da ‘hesaplanamaz’ sayılar denir.
Cebir ve Trigonometri denklemleri gibi bir takım matematik formüllerini uygulayabilen Turing makineleri olabilir. Gereken tek şey matematik sembollerin ikilik sistemde kodlanması ve bir Turing makinesına uygulanmasıdır. Bu durum, matematik sorularına elde edilecek bir algoritmik yapı sayesinde cevap arayan Hilbert problemini akla getirir.
Aşağıdan Alan Turing ile ilgili videoyu izleyebilirsiniz.